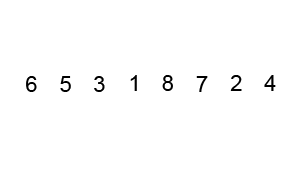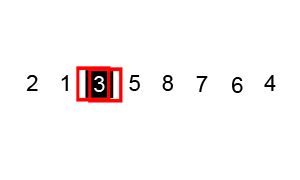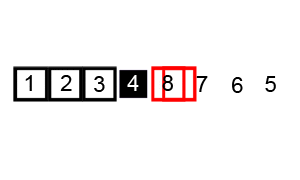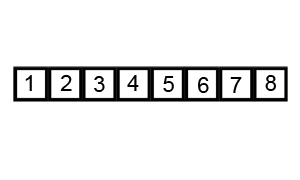Quick Sort

Explanation:

Pick a pivot element from the list. Go through the remaining elements and split them into two groups, ones smaller than the pivot and ones bigger than the pivot. Put the pivot between those two groups, so it ends up in its final spot. Repeat the same process (including pivot picking) on the left and right groups until all the groups are size one or empty, then the whole list is sorted.

• Nearly Sorted Data: Quicksort minimizes unnecessary swaps, it swaps nothing if the data is already sorted.
• Choosing Pivot: If the pivot is close to the median, the list splits into two similar-sized parts and quick sort stays fast (O(n log(n))). If the pivot is near the smallest or largest, almost everything goes to one side, so quick sort repeats the partition step on nearly the whole list over and over, which can make it much slower (O(n^2)).

Implementation:

function quickSort(arr, left = 0, right = arr.length - 1) {
  if (left < right) {
    const pivot = arr[Math.floor((left + right) / 2)]; // chosen pivot: always the middle element

    const index = partition(arr, left, right, pivot);

    quickSort(arr, left, index - 1);
    quickSort(arr, index, right);
  }

  return arr;
}

function partition(arr, left, right, pivot) {
  while (left <= right) {
    while (arr[left] < pivot) {
      left++;
    }

    while (arr[right] > pivot) {
      right--;
    }

    if (left <= right) {
      [arr[left], arr[right]] = [arr[right], arr[left]];

      left++;
      right--;
    }
  }

  return left;
}

const numbers = [6, 5, 3, 1, 8, 7, 2, 4];

quickSort(numbers);

console.log(numbers); // [1, 2, 3, 4, 5, 6, 7, 8]