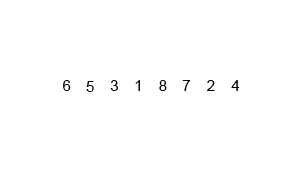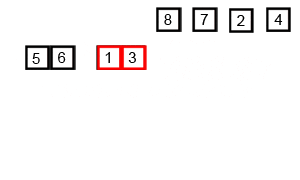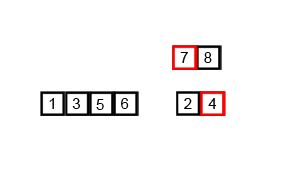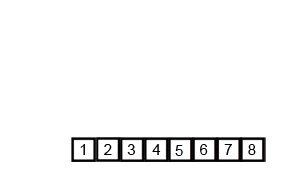Merge Sort

Stable?	Time	Space
Yes	`O(n log(n))`	`O(n)`

Explanation:

Split the list into two halves, then keep splitting each half until you end up with single-element lists. Treat each single element as already sorted, then merge pairs back together by comparing the front elements of each list and taking the smaller one first. Keep merging the sorted pieces into bigger sorted lists until everything is merged into one fully sorted list.

Parallelization: Merge sort is parallel-friendly because, after splitting, the two halves can be sorted independently and concurrently across multiple CPU cores.

Predictable: Merge sort consistently performs well regardless of input order, providing reliable worst-case performance for large datasets.

Implementation:

Merge Sort

function mergeSort(arr) {
  if (arr.length <= 1) return arr;

  const mid = Math.floor(arr.length / 2);
  const left = arr.slice(0, mid);
  const right = arr.slice(mid);

  // split until base case and then merge back while unfolding:
  return merge(mergeSort(left), mergeSort(right));
}

// compare and merge:
function merge(left, right) {
  const tmp = [];

  let l = 0;
  let r = 0;

  while (l < left.length && r < right.length) {
    if (left[l] <= right[r]) {
      tmp.push(left[l]);
      l++;
    } else {
      tmp.push(right[r]);
      r++;
    }
  }

  return [...tmp, ...left.slice(l), ...right.slice(r)];
}

const numbers = [6, 5, 3, 1, 8, 7, 2, 4];

console.log(mergeSort(numbers)); // [1, 2, 3, 4, 5, 6, 7, 8]